Solução MNPEF 2014 (em construção)

Questão 01. Duas bolas, 1 e 2, são lançadas simultaneamente do mesmo ponto em um plano horizontal. Efeitos do ar são desprezíveis de modo que após o lançamento a única ação sobre a bola é a da gravidade. A bola 1 descreve uma parábola que vai mais alto que a descrita pela bola 2. Já a bola 2 cai mais longe que a 1, como é mostrado pelas trajetórias na figura abaixo.

Nesta situação, é correto afirmar que:

A) a bola 1 fica menos tempo no ar que a bola 2.

B) a bola 1 fica mais tempo no ar que a bola 2.

C) as duas bolas ficam o mesmo tempo no ar.

D) é impossível dizer qual das bolas cairá primeiro sem conhecer suas velocidades iniciais.

Questão 02. Uma partícula move-se em linha reta sob a ação de uma força resultante que lhe fornece uma potência constante (ou seja, o trabalho por unidade de tempo realizado pela força sobre a partícula é constante). A partícula está em repouso em t = 0 s, e em t = 1 s a sua velocidade é 1 m/s. Em t = 4 s, a velocidade da partícula é

A) 2 m/s.

B) 4 m/s.

C) 6 m/s.

D) 8 m/s.

Questão 03. Um cilindro maciço, indeformável e homogêneo pode girar sem atrito em torno de um eixo que passa pelo seu centro. O eixo está fixo a uma plataforma que pode mover-se livremente num plano horizontal. Com a plataforma inicialmente em repouso, uma bala deformável é disparada e quando atinge o cilindro tem velocidade horizontal V. Após a colisão com o cilindro a bala cai sobre a plataforma e fica em repouso sobre esta. A bala pode atingir o cilindro acima do eixo, na altura do eixo ou abaixo deste, sempre com a mesma velocidade V. Essas três situações estão indicadas na figura. Na situação 1 a bala coloca o cilindro em rotação anti-horária, na 2 deixa-o sem girar, e na 3 produz uma rotação no sentido horário.

Após o impacto e queda da bala o módulo da velocidade da plataforma é V1, V2 ou V3, dependendo da situação escolhida (1, 2 ou 3, respectivamente). Sobre essas velocidades, podemos afirmar que

A) V1 > V2 > V3

B) V1 < V2 < V3

C) V1 = V2 = V3

D) V1 = V3 < V2

Solução:

Para as três situações a bala transfere momento linear para o sistema, como em todos os casos: “após a colisão com o cilindro a bala cai sobre a plataforma e fica em repouso sobre esta”, a quantidade de momento transferida para o sistema é a mesma. Com relação à Energia Cinética, esta não é conservada uma vez que a colisão da bala com o sistema com é do tipo plástico.

Questão 04. A velocidade de descida de uma escada rolante é de 1 degrau por segundo. Uma criança resolve subir (não descer) essa escada, escalando 2 degraus a cada segundo. Se a escada estivesse parada, a criança subiria 20 degraus para chegar ao alto. Com a escada em movimento a criança sobe

A) 10 degraus.

B) 20 degraus.

C) 30 degraus.

D) 40 degraus.

Solução:

A cada um segundo, a criança sobe dois degraus e a escada desce um, portanto, como resultado a criança sobe com velocidade de 1 degrau por segundo. Como a distancia de subida corresponde a 20 degraus, e, a cada 1 degrau que a criança sobe, a criança caminha 2, para subir os 20 degraus a criança caminha 40.

Questão 05. A órbita da Lua no sistema de referência da Terra é uma elipse, sendo a distância de máxima aproximação (perigeu) da Lua à Terra cerca de 56R e a distância de máximo afastamento (apogeu) da Lua à Terra cerca 65R, onde R é o raio da Terra. Na figura abaixo está representada a órbita bem como os vetores força gravitacional exercida na Lua pela Terra e velocidade da Lua em um ponto da órbita.

Sendo os módulos das velocidades V_A e V_P e das forças gravitacionais F_A e F_P respectivamente no apogeu (A) e no perigeu (P) afirma-se que

I) 56.V_P = 65.V_A.

II) F_P > F_A.

III) Os vetores força gravitacional exercida na Lua e velocidade orbital da Lua são ortogonais entre si em qualquer ponto da órbita.

Quais das afirmações são corretas?

A) I e III.

B) I, II, e III.

C) II e III.

D) I e II.

Solução:

I) Como não se trata de um movimento circular, não se pode igualar a força gravitacional à resultante centrípeta. Parte-se do princípio da conservação do momento angular L:

L_A = L_P

M_Lua V_A d_A sen 90 = M_Lua V_P d_P sen 90

65RV_A = 56RV_P

Logo 56V_P = 65V_A

II) Da Lei da Gravitação Universal de Isaac Newton:

F_G ∝ d^–2

Como d_A > d_P, e a força é inversamente proporcional ao quadrado da distância, conclui-se que: F_P > F_A.

III) Como a orbita é elíptica, os vetores velocidade orbital (tangencial à trajetória) da Lua e força gravitacional exercida na Lua são ortogonais apenas no Perigeu e no Apogeu.

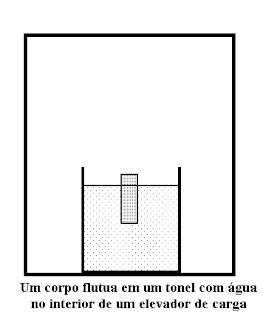
Questão 06. Um tonel contendo água está em repouso em relação ao assoalho horizontal de um elevador. No interior do tonel flutua na água um objeto conforme mostra a figura abaixo, sendo γ a fração do volume do objeto que se encontra abaixo do nível da água.

Considere as seguintes possibilidades para o movimento do elevador:

I) O elevador se encontra em repouso no sistema de referência da Terra.

II) O elevador se encontra acelerado verticalmente para cima no sistema de referência da Terra.

Sobre a pressão exercida pela água no fundo do tonel e sobre a fração γ do volume do objeto, qual das alternativas é correta?

A) Na situação I a pressão é menor do que na situação II. Na situação I a fração γ é menor do que na situação II.

B) Na situação I a pressão é a mesma do que na situação II. Na situação I a fração γ é menor do que na situação II.

C) Na situação I a pressão é menor do que na situação II. Na situação I a fração γ é a mesma que na situação II.

D) Na situação I a pressão é a mesma do que na situação II. Na situação I a fração γ é a mesma que na situação II.

Solução:

Para a situação I, como o elevador fica em repouso no sistema de referência da Terra a pressão hidrostática é definida por:

p_I = ρgh

Em que ρ corresponde à densidade da água, g ao módulo da aceleração local da gravidade e h à profundidade em relação à superfície livre do líquido. Para o objeto flutuando no líquido, cujo volume submerso é γ:

E = P ⟹ ργ_Ig = mg ⟹ γ_I = m/ρ

Para a situação II, devido à Inércia, a aceleração sofrida no interior do elevador é

g' = g + a

Em que a corresponde ao módulo da aceleração do elevador, a pressão hidrostática é:

p_II = ρg'h

Para o objeto flutuando:

E = P ⟹ ργ_IIg' = mg' ⟹γ_II = m/ρ

Como g' > g, conclui-se que p_II > p_I, e, γ_I = γ_II.

Questão 07. Água carregando umas poucas bolhas de ar passa por uma tubulação horizontal. O tubo, que está completamente cheio pela água corrente, sofre um estreitamento como o mostrado na figura.

Quando entram na seção mais estreita do tubo, as bolhas

A) desaparecem.

B) ficam menores do que eram na seção larga.

C) mantêm o tamanho que tinham na seção larga.

D) ficam maiores do que eram na seção larga.

Questão 08. Duas cordas vibrantes (1 e 2), presas pelas extremidades, são feitas do mesmo material e têm o mesmo comprimento. O diâmetro da corda 1 é duas vezes maior que o diâmetro da corda 2. O módulo da força tensora nas cordas 1 e 2 é, respectivamente, T₁ e T₂. Para que as duas cordas vibrem com a mesma frequência fundamental, devemos ter

A) T₁ = 6 T₂.

B) T₁ = 4 T₂.

C) T₁ = 2 T₂.

D) T₁ = T₂.

Questão 09. Intensidades sonoras acima de 1,0 W/m² podem produzir sensações auditivas dolorosas e danos no aparelho auditivo humano. Suponha que intensidades mais baixas que essa são seguras para nós. Considere uma fonte sonora com potência média de 200 W, emitindo uniformemente em todas as direções. Desprezando ecos, reverberações e perdas de energia sonora para o ar, a menor distância que alguém pode chegar dessa fonte sem sofrer sensações auditivas dolorosas é de aproximadamente:

A) 1 cm.

B) 20 cm.

C) 4 m.

D) 200 m.

Questão 10. Um astrônomo observa que todo o espectro de absorção de uma estrela próxima encontra-se deslocado para comprimentos de onda menores que os previstos a partir da composição química esperada nessa estrela. Isso significa que:

A) a estrela está se aproximando do Sistema Solar.

B) a estrela está se afastando do Sistema Solar.

C) a estrela está praticamente em repouso relativo ao Sistema Solar.

D) na estrela existem elementos químicos que não são encontrados no Sol.

Questão 11. Dois pulsos de onda propagam-se sem dispersão ao longo de uma linha reta, aproximando-se um do outro. O módulo da velocidade de propagação dos pulsos é V. No instante t = 0 a forma da onda é a mostrada na figura abaixo. Nesse instante ainda não há superposição entre os dois pulsos e a distância entre os mínimos que os lideram é D.

No instante t = D / (2V) a forma da onda é dada por

Questão 14. No circuito esquematizado L₁, L₂ e L₃ são lâmpadas com as mesmas características de tensão de operação e potência. Sabe-se que o brilho do filamento de qualquer lâmpada depende da intensidade da corrente elétrica no filamento.

Quando a chave é fechada constata-se que a lâmpada L₁ passa a brilhar. Sobre o brilho das lâmpadas pode-se afirmar então que:

 

A) L₁ brilha mais do que L₂ e apresenta o mesmo brilho de L₃.

B) L₁ brilha tanto quanto L₂ e apresenta brilho menor do que L₃.

C) L₁ brilha menos do que L₂ e apresenta o mesmo brilho de L₃.

D) L₁ brilha tanto quanto L₂ e apresenta brilho maior do que L₃.

SOLUÇÃO:

As três lâmpadas apresentam as mesmas características, logo R₁ = R₂ = R₃ = R. L₃ está submetida à tensão U, da lei de ohm, tem-se que a corrente elétrica que passa por L₃ é i₃ = U/R. Como L₁ está em série com L₂, a resistência equivalente da série é R_1,2 = 2R, logo a corrente que passa pela série é i_1,2 = U/2R (no circuito série a corrente em cada componente é a corrente equivalente, portanto: i_1,2 = i₁ = i₂). Da definição de potência desenvolvida P = Ui, obtém-se que P₁ = P₂ = P₃/2 = U²/2R. Quanto maior a potência desenvolvida na lâmpada, maior será o brilho emitido pela mesma, como P₁ = P₂ < P₃, conclui-se que L₁ brilha tanto quanto L₂ e apresenta brilho menor do que L₃.

Questão 15. Considere o circuito esquematizado. Após o fechamento da chave, quando o regime estacionário foi atingido, a intensidade da corrente na fonte é 3,0 A.

Qual é então a fem da fonte e a diferença de potencial no capacitor?

 

A) 120 V e 120 V.

B) 120 V e 60 V.

C) 180 V e 120 V.

D) 180V e 60 V.

SOLUÇÃO:

No regime estacionário o capacitor C já está totalmente carregado, deste modo não há circuitação de corrente no capacitor. Pode-se reduzir o circuito a dois resistores em série percorridos pela corrente elétrica i = 3,0 A, sendo R₁ = 40 Ω e por R₂ = 20 Ω. A resistência equivalente do circuito série é R = R₁ + R₂ = 60 Ω. Da Lei de Ohm a U₁ = R₁i = 120 V, e, U₂ = R₂i = 60 V. A tensão equivalente no circuito série é U = U₁ + U₂ = 180 V, como o capacitor está em paralelo com o resistor R₂, a tensão no capacitor é U_C = U₂ = 60 V.

Questão 16. No circuito representado na figura o capacitor C₁ está carregado e a diferença de potencial elétrico entre as suas placas é 12 V. O capacitor C₂ está descarregado. Depois que a chave é fechada e o circuito atingiu novamente o equilíbrio eletrostático a diferença de potencial entre as placas do capacitor C₁ diminui para 4,0 V.

Qual é a diferença de potencial entre as placas do capacitor C₂ e a energia eletrostática armazenada no circuito na nova situação de equilíbrio eletrostático?

 

A) A diferença de potencial entre as placas do capacitor C₂ é 4,0 V e a energia eletrostática no circuito é menor do que antes de a chave ser fechada.

B) A diferença de potencial entre as placas do capacitor C₂ é 8,0 V e a energia eletrostática no circuito continua a mesma que antes de a chave ser fechada.

C) A diferença de potencial entre as placas do capacitor C₂ é 4,0 V e a energia eletrostática no circuito continua a mesma que antes de a chave ser fechada.

D) A diferença de potencial entre as placas do capacitor C₂ é 8,0 V e a energia eletrostática no circuito é menor do que antes de a chave ser fechada.

SOLUÇÃO:

Quando a chave é fechada, os capacitores 1 e 2 estão associados em paralelo. Na associação em paralelo U₁ = U₂ = 4,0 V. A energia eletrostática armazenada num capacitor equivalente é definida por E = QV/2. Antes da chave ser fechada E₀ = 6Q₁, após o fechamento da chave (da conservação da carga, Q’ = Q₁), na nova situação de equilíbrio eletrostático E = 2Q₁ = E₀/3. Portanto, após a situação de equilíbrio eletrostático, a diferença de potencial entre as placas do capacitor C₂ é 4,0 V e a energia eletrostática no circuito é menor do que antes de a chave ser fechada.

Questão 17. Duas espiras condutoras, contidas em planos paralelos entre si conforme a figura, são percorridas por correntes alternadas com a mesma frequência e diferentes fases. As correntes em t = 0 estão representadas na figura e o gráfico indica como tais correntes se modificam no tempo.

 

As seguintes afirmativas são feitas sobre as espiras:

I) A frequência das correntes alternadas é 111 Hz.

II) Em um ciclo completo de corrente a força magnética média entre ambas as espiras é atrativa.

III) No intervalo t > 1 ms e t < 2 ms ocorre repulsão entre as espiras.

Qual(is) das afirmativas é(são) correta(s)?

A) I e II.

B) II e III.

C) Apenas a I.

D) Apenas a III.

SOLUÇÃO:

I) Da análise do gráfico, observa-se que o período das correntes é T = 8.10^–3 s, como a frequência é f = 1/T, obtém-se que o valor da frequência das correntes é f = 125 Hz ≠ 111 Hz.

II) Quando as correntes de dois fios condutores possuem mesmos sentidos, a interação entre os fios é de atração, no entanto, se os sentidos das correntes nos fios forem contrários, a interação será de repulsão. Como visto no gráfico, na maior parte do tempo (com exceção do intervalo entre 1 ms e 2 ms) as correntes possuem mesmos sentidos, portanto a força magnética média entre as espiras é de atração.

III) Conforme apresentado no item II, no intervalo de tempo 1 < t(ms) < 2 ocorre repulsão entre as espiras, pois as correntes nas espiras possuem sentidos contrários.

Questão 18. Uma espira condutora é alimentada por uma corrente alternada i₁ que varia no tempo de acordo com a função i₁ = 3 sen(10πt), onde i₁ é a corrente em amperes e t é o tempo em segundos. Uma segunda espira condutora, interrompida por um isolante, está colocada muito próxima da primeira espira (vide figura) de tal forma que os eixos de simetria de ambas as espiras sejam coincidentes.

Qual dos gráficos que seguem melhor representa a força eletromotriz induzida (fem) em função do tempo na segunda espira?

 SOLUÇÃO:

O campo magnético induzido na espira 1 é:

B = (μi₁)/2r = B₀ sen(10πt)

O fluxo magnético que passa na espira 2 é Φ_B = B.S.cos α, em que B é o módulo do campo magnético, S é a área da espira 2 e α é o ângulo entre o vetor B e a direção normal da superfície S limitada pela espira 2. Como os eixos de simetria das espiras é coincidente cos α = cos 0 = 1. A fem induzida na espira 2 é:

ε(t) = – dΦ_B)/dt

ε(t) = – ε₀ cos(10πt)

Comparando a expressão obtida com a função de onda x(t) = A cos(ωt), obtém-se que ω = 10π. Como a frequência angular é definida por ω = 2πf, então a frequência da fem induzida na espira 2 é f = 5 Hz. O período de ε(t) é T = 1/f = 0,2 s. portanto o gráfico que melhor representa ε(t) na espira 2 é expresso na alternativa (B)

Questão 19. Um par de lâminas bimetálicas se apresenta sem deformação a 25º C conforme a figura. Uma das partes de cada par é constituída pelo mesmo metal (metal 1), sendo a segunda parte de cada lâmina bimetálica constituída por metais diversos (metal 2 e metal 3). Ao baixar a temperatura para 10º C as duas lâminas se deformam em acordo com o que está representado na figura.

Sendo α₁, α₂ e α₃ respectivamente os coeficientes de dilatação linear do metal 1, do metal 2 e do metal 3, a relação entre estes coeficientes é

A) α₁ < α₂ e α₂ > α₃.

B) α₁ > α₃ e α₃ < α₂.

C) α₂ < α₁ e α₁ < α₃.

D) α₂ > α₁ e α₁ > α₃.

SOLUÇÃO:

O material com maior coeficiente de dilatação linear α é o que dilata mais (pode ser contração ou expansão) em virtude de determinada variação de temperatura. No caso da diminuição de temperatura (de 25 °C para 10 °C), o material que contrai mais é o que possui maior coeficiente de dilatação linear. Do lado esquerdo da figura, observa-se que α₁ > α₂, e, α₃ > α₁. Logo, comparando os coeficientes de dilatação linear dos três materiais, tem-se que: α₂ < α₁ < α₃.

Questão 20. Um aquecedor de água residencial de passagem é constituído por uma serpentina que recebe água na temperatura ambiente. A água que circula pela serpentina é aquecida com auxílio de um queimador de gás. Quando o aquecedor funciona em regime estacionário, com uma vazão de água na serpentina de 10,0 L.min^-1, a água entra a 20 ºC e sai da serpentina a 40 ºC. A queima de 1,0 g de gás libera em energia cerca de 10 kcal, sendo efetivamente transferida a para água na serpentina cerca 40% dessa quantidade de energia. Sabe-se que o calor específico da água é 1,0 kcal.kg^-1.ºC^-1 e sua massa específica é 1,0 kg.L^-1. Se o aquecedor é utilizado durante 1 h para aquecer a água, qual é aproximadamente a massa de gás queimada?

A) 0,50 kg

B) 1,2 kg

C) 3,0 kg

D) 6,0 kg

SOLUÇÃO:

Se a cada minuto circulam 10 L de água pela serpentina, em 1 h devem circular um volume de 600 L de água pela serpentina. Como a massa específica da água é 1 kg.L^-1, a massa que é aquecida (durante 1 h) na serpentina é m = 600 kg. Da equação fundamental da calorimetria:

Q = mcΔθ

Q = 600.1.(40 – 20)

Q = 12000 kcal

OBS: a massa é expressa em kg, e, o calor específico em kcal.kg^-1.°C^-1, logo, a quantidade de calor obtida para aquecer a água é Q = 12000 kcal.

Como 40% da energia proveniente da queima do gás é utilizada para aquecer a água, a energia total liberada pela queima do gás é X (kcal), tal que:

X/12000 = 100%/40%

X = 30000 kcal

Se cada 1 g = 0,001 kg de gás queimado libera 10 kcal de energia, a massa M (kg), de queimado para liberar 30000 kcal de energia é obtida por:

M/0,001 = 30000/10

M = 3,0 kg

Portanto, em 1 h, o consumo de gás é equivalente a 3,0 kg.

Questão 21. Um ciclo reversível é operado com uma a amostra de gás ideal em acordo com o diagrama pressão versus volume que segue.

A transformação BC é uma adiabática e nessa transformação o gás realiza um trabalho de 6,2 atm.L. Qual é o trabalho no ciclo?

A) 5,2 atm.L

B) 11,2 atm.L

C) 15,2 atm.L

D) 17,2 atm.L

SOLUÇÃO:

O trabalho pode ser obtido pela área do gráfico p x V.

Na etapa AB, tem-se uma expansão (na expansão o trabalho é realizado pelo gás e tem sinal positivo) isobárica (p constante), logo W = pΔV = 5.(2 – 1) = 5 atm.L.

Na etapa BC, (conforme o enunciado) tem-se uma expansão (W₊) adiabática (Q = 0), em que o trabalho realizado (pelo gás) é W = 6,2 atm.L

Na etapa CD, tem-se uma compressão (W_-) isobárica, o trabalho realizado (sobre o gás) é W = – pΔV = – 2.(4 – 1) = – 6 atm.L.

A etapa DA é uma transformação isocórica (V constante), portanto não há realização de trabalho.

O trabalho realizado por um ciclo completo é W = 5 + 6,2 – 6 = 5,2 atm.L.

Questão 22. Um ciclo reversível é operado com uma a amostra de gás ideal em acordo com o diagrama pressão versus volume que segue.

A transformação BC é uma adiabática, isto é, o gás não troca calor com o entorno. Sobre a temperatura na transformação BC e o calor trocado pelo gás com o entorno na transformação DA afirma-se que

A) a temperatura permanece constante e o gás absorve calor.

B) a temperatura diminui e o gás absorve calor.

C) a temperatura permanece constante e o gás cede calor.

D) a temperatura diminui e o gás cede calor.

SOLUÇÃO:

A etapa BC corresponde à uma expansão (ΔV > 0, o trabalho é realizado pelo gás e positivo) adiabática (Q = 0). Da primeira lei da termodinâmica:

ΔU = Q – W

ΔU = 0 – W

ΔU_– = – W₊

ΔU < 0

Percebe-se que a variação da energia interna é negativa. Como a energia interna é proporcional à temperatura (U = 3nRT/2), se ΔU < 0, então a variação da temperatura também é negativa (ΔT < 0). Portanto na etapa BC ocorre diminuição da temperatura. O gás utiliza a própria energia interna para expandir adiabaticamente.

A etapa DA corresponde à uma transformação isocórica (ΔV = 0 e W = 0). Da Lei geral dos gases (p_DV_D/T_D = p_AV_A/T_A) observa-se que para que a pressão aumente a volume constante, a temperatura deve ser aumentada proporcionalmente. No aquecimento do gás tanto a temperatura, quanto a energia interna aumentam, da análise matemática da primeira lei da termodinâmica:

ΔU = Q – W

ΔU = Q – 0

Q₊ = ΔU₊

Q > 0

Na etapa DA o gás recebe calor

Questão 23. Um apontador laser emite luz vermelha e outro emite luz verde, ambos produzindo feixes de radiação com a mesma potência de 5 mW. Sobre estes dois apontadores afirma-se que:

I) Um fóton do apontador vermelho possui mais energia do que um fóton do apontador verde.

II) Na água a luz do apontador verde tem rapidez (velocidade de fase) diferente da rapidez da luz do apontador vermelho.

III) O número de fótons emitidos na unidade de tempo para o apontador vermelho é maior do que para o apontador verde.

Qual(is) das afirmativas é(são) correta(s)?

A) Apenas I.

B) Apenas II.

C) I e II.

D) II e III.

SOLUÇÃO:

I) Um fóton possui energia definida por E = hf, em que h é a constante de Planck e f é a frequência da respectiva radiação eletromagnética. Como f_verde > f_vermelho, então a relação de energia E dos fótons emitidos é E_verde > E_vermelho.

II) Num meio cujo índice de refração é n = c/v (c é a velocidade da luz no vácuo e v é a velocidade de fase da luz no respectivo meio). Da lei de Snell-Descartes:

n_I sen θ_I = n_T sen θ_T

Em que n_I é o índice de refração no ar, n_T é o índice de refração na água, θ_I é o ângulo de incidência e θ_T é o ângulo de transmissão. Na dispersão da luz, observa-se que θ_T(vermelho) > θ_T(verde), logo sen θ_T(vermelho) > sen θ_T(verde). Disto conclui-se que n_T(vermelho) < n_T(verde). Para a luz vermelha v_T(vermelho) = c/n_T(vermelho), e, para a luz verde v_T(verde) = c/n_T(vede), portanto, na água v_vermelho > v_verde.

OBS: é difícil de perceber a dispersão da luz na água, portanto a diferença de velocidades de fases é pequena.

III) Como as potências dos apontadores são equivalentes (5 mW), da definição de potência P = E/Δt (energia por unidade de tempo), tem-se que a quantidade total de energia emitida pelos apontadores deve ser igual num mesmo intervalo de tempo. Em que a energia total de n fótons emitidos é definida como E_n = nhf, como f_verde > f_vermelho, então n_vermelho > n_verde.

Questão 24. Em um experimento de difração um feixe de elétrons incide sobre um anteparo com duas fendas A e B. No ponto P há um detector de elétrons que mede a intensidade de 36 elétrons por segundo quando apenas a fenda A está aberta e a intensidade de 16 elétrons por segundo quando apenas a fenda B está aberta.

Quando ambas as fendas estiverem abertas a intensidade I em elétrons por segundo em P está compreendida no intervalo

 

A) 4 ≤ I ≤ 100.

B) 20 ≤ I ≤ 52.

C) 0 ≤ I ≤ 52.

D) 16 ≤ I ≤ 36.

SOLUÇÃO:

Trata-se de um experimento de dupla fenda. Quando a fenda A está aberta, a intensidade de onda no ponto P é dada pelo módulo da amplitude da onda ao quadrado I_A(x) = |φ_A(x)|². Quando a fenda B está aberta I_B(x) = |φ_B(x)|². Quando as duas fendas estão abertas:

I_AB(x) = |φ_A(x) + φ_B(x)|² = I_A + I_B +2(I_A.I_B)^1/2 cos θ

Em que cos θ da a diferença de fase entre as contribuições das duas frentes de ondas que resultam da difração da onda original nas fendas. O último termo é o de interferência. Com I_A = 36 e I_B = 16, e – 1 ≤ cos θ ≤ + 1:

I_AB(Máxima) = 36 + 16 – 2(36.16)^1/2 = 4

I_AB(Máxima) = 36 + 16 + 2(36.16)^1/2 = 100

Portanto a intensidade no ponto P com as duas fendas abertas é tal que: 4 ≤ I ≤ 100.